Undirected graph
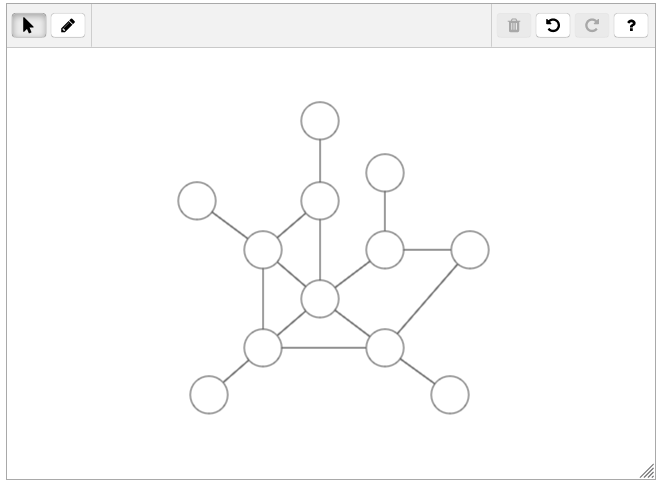
"Draw an undirected graph with diameter at most 4 and degree sequence (1,1,1,1,1,2,3,3,4,4,4,5)."
Directed graph
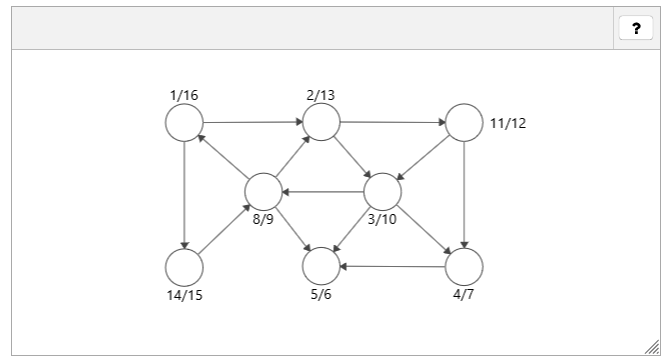
"We have run DFS on the graph given below. The start and finish times are written next to each node. Highlight all the cross edges."
Finite-state machine
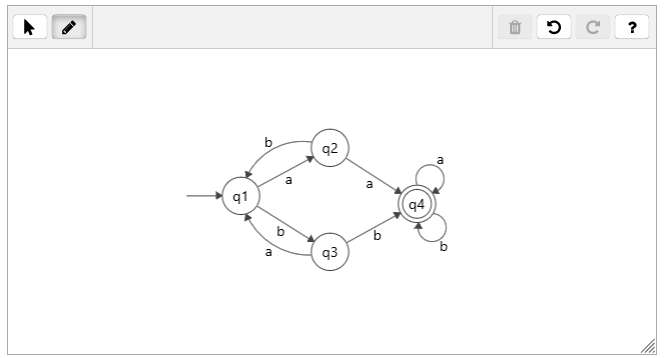
"Provide a DFA with no more than 4 states that accepts the language {w in {a,b}* | w has a substring aa and/or a substring bb}."
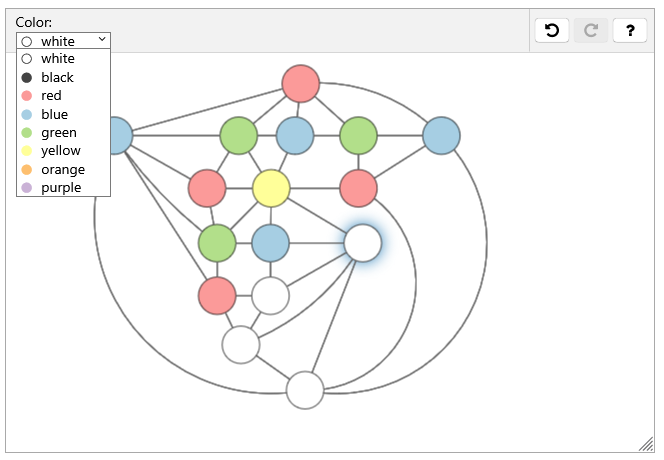
Coloring
"Color the graph such that the result is a valid coloring with the minimal number of colors."
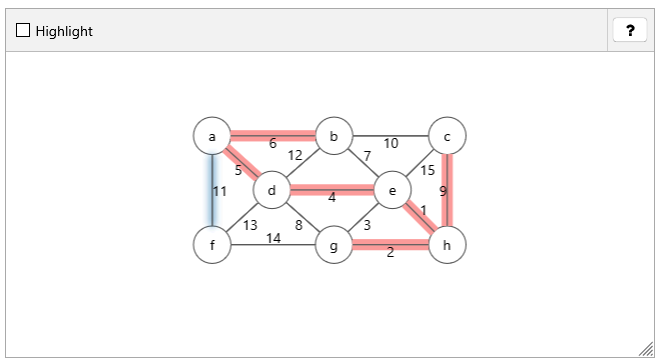
Highlighting
"Highlight a set of edges that together form a minimum spanning tree of the given graph."
Preload
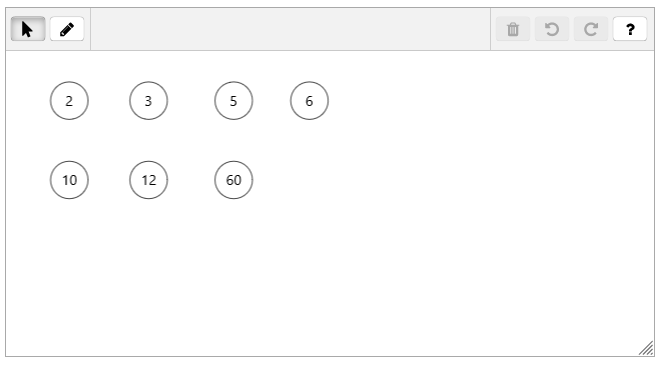
"Draw the Hasse diagram for the divisibility operation on the given set of elements."